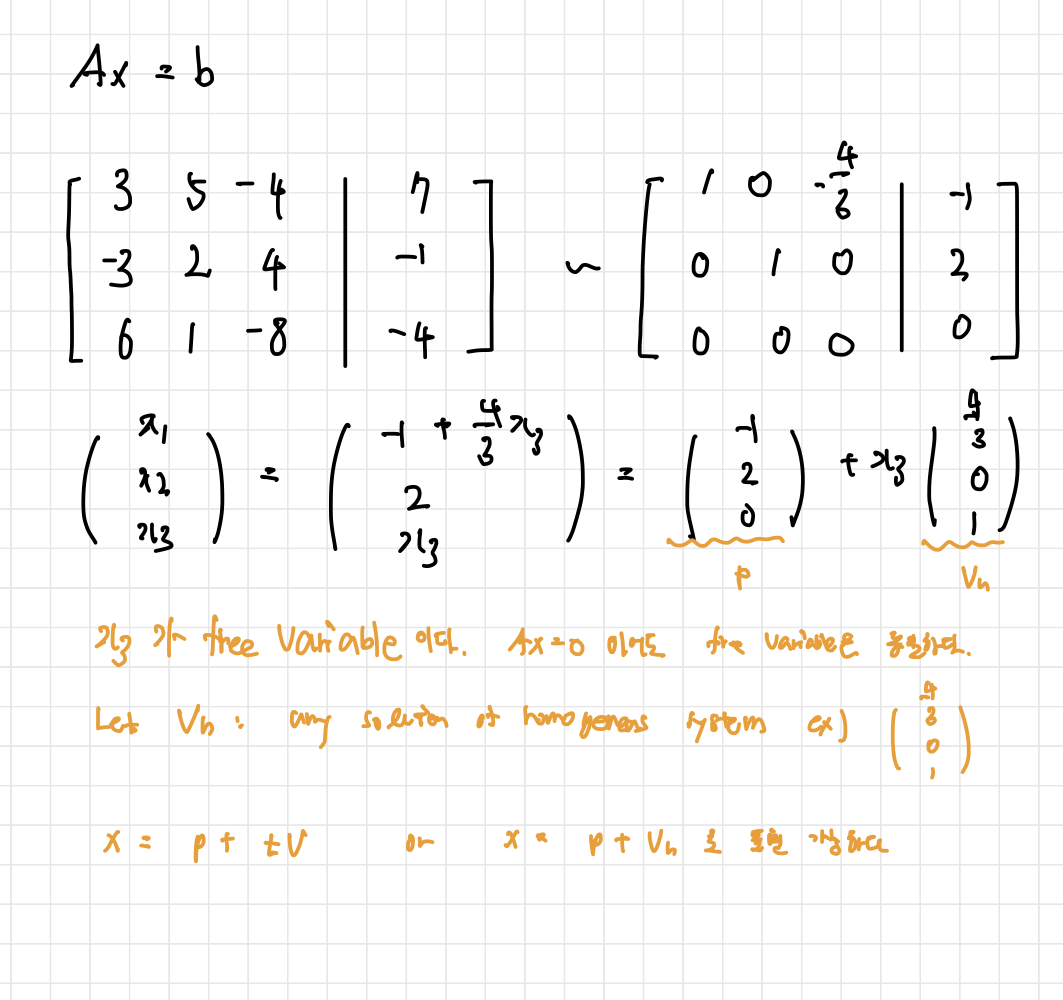01. Linear Equation

Linear Equation

\[\begin{bmatrix} 1 & 1 & 1 \end{bmatrix}\]

equivalent if the system has same solution set

A system of linear equations has either

no solution or

unique solution or

inf many solution

coefficient matrix

augement matrix

Elementary row operations

1. scaling
2. interchaning
3. scaling

row equivalent

1. coefficent matrix 에 row equivalnet ⇒ row operations 거치면 같다
2. augmented matrix에 row equivalent ⇒ row operations해도 solution set 동일하다

EF vs REF vs RREF

EF

1. 모든 원소가 0인 행렬 맨 아래로

2. leading entry of a row shoud be in a column to the right of the leading entry of the row above it.

REF

(leading 1 등장)

1. 0이 아닌 원소를 갖는 행에서 맨 처음 나오는 0이 아닌 수는 1이어야 한다. 이러한 1을 선도 1(leading one)이라고 한다.

2. 모든 원소가 0인 행은 행렬의 맨 아래로 내려가야 한다.

3. 0이 아닌 원소를 갖는 연속된 두 행은 해당 행의 leading 1이 윗 행의 leading 1보다 오른쪽에 있어야 한다.

RREF

REF +

1. Each leading 1 is the only nonzero entroy in its column

leading variable

free variable

Uniqueness of the reduced echelon form

1. inconsistent

   1. [ 0000

      b ] b≠ 0 : augement column is a pivot column in an echelon form

2. consistent : pivot in every row in coffecient part
   1. no free variable

      1. pivot in every column in coefficnet part in echelon form

         (이 말이 사실 linear independent와 동일하다)

      2. number of pivot columns are same as number of variables

   2. free variable

How to make RREF form

1. forward phase (making REF)
2. backward phase (making RREF)

Homogeneous

\[Ax=0\]

at least trivial solution x = 0

only trivial solution when A has inverse : determinant ≠ 0

non - homogeneous

unique solution → pivot in every column (correct)

이때는 [ 00000

b ]일 수 없다. consistent해야하니깐

pivot in every column → unique solution (incorrect)

[ 0000

b]꼴이여도 pivot in every column 이다

homogeneous

unique solution ←→ pivot in every column (correct)

[ 00000

b ] 불가능 ⇒ 즉 always consistent due to trivial solution

[ 00000

0 ] 이경우에는 pivot이 없다.

따라서 unique solution이 없으려면 free variable이 없어야한다.

Parametric vector form